ტესტები
პუასონის ამოცანა, რომელსაც ჰოლივუდის ბლოკბასტერებში და Microsoft–ის ინტერვიუებში ხსნიან

სიმეონ დენი პუასონი, ფრანგი მათემატიკოსი, ცხოვრების გზის არჩევაზე დიდხანს ყოყმანობდა, სანამ მეგობარმა არ აჩვენა ეშმაკური ამოცანა ჭურჭლებში სითხის გადასხმის შესახებ, რომელიც თავად ვერ ამოხსნა. ახალგაზრდა პუასონმა გამოსავალი 1 საათზე ნაკლებ დროში იპოვა. შედეგად მათემატიკოსობა მტკიცედ გადაწყვიტა. ამოცანას, რომელმაც მისი ცხოვრება განსაზღვრა, „პუასონის ამოცანა“ უწოდეს.

დღეს მსგავსი ამოცანები ფართოდ გავრცელებულია. ასეთი ამოცანები შეიძლება Google–ის и Microsoft–ის გასაუბრებებზე შეგხვდეთ. ერთ–ერთი მათგანის ამოხსნა ბრიუს უილისის გმირს ჰოლივუდის ბლოკბასტერის „კერკეტი კაკალი 3“ ეკრანზე მოუწია. შეძლებთ სითხის გადასხმაზე ამოცანის ისე მარტივად ამოხსნას, როგორც ეს პუასონმა და ჯონ მაკლეინმა გააკეთეს? პატარა სპოილერი: გაჩვენებთ, როგორ ამოხსნათ პუასონის ამოცანა მარტივად, პროგრამირების და ბილიარდის პრინციპის გამოყენებით.
პუასონის ამოცანა
სატესტო დავალება Microsoft-გან
“თქვენ გაქვთ წყლის უსასრულო რეზერვი და 2 ვედრო: ერთი ვედრო ხუთლიტრიანია, მეორე – 3–იანი. ზუსტად 4 ლ უნდა გაზომოთ. როგორ გააკეთებთ?” დავიწყოთ უილისის საზრიანი კინოგმირის მსგავსად მსჯელობა.
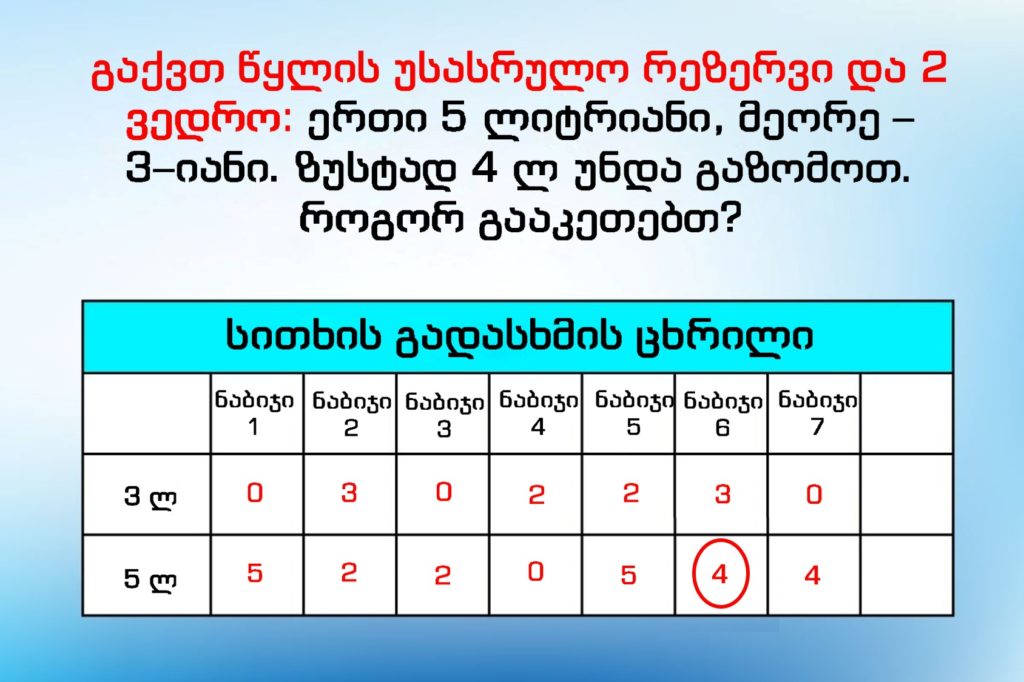
ცხადია, რომ 4 ლ პატარა ვედროში ვერ ჩაეტევა. გამოდის, რომ ჯერ ხუთლიტრიანი ვედრო წყლით უნდა გაავსოთ. შემდეგ ლოგიკურია, რომ აქედან პატარა ვედრო გაავსოთ. ახლა პატარა ვედრო გავსებულია, ხოლო დიდში 2 ლ დარჩა და მოიცადეთ. ახლა გონებაში ყველა შესაძლო ვარიანტის განხილვა რთულია. სწორედ ამიტომ, ამოცანის ცდის და შეცდომის ხარჯზე ამოხსნა ყველას არ შეუძლია. იქ, სადაც შთაგონება საკმარისი არაა, ალგორითმი დაგეხმარებათ.
ბლოკ–სქემის მეთოდი
თუ Microsoft-ში დასაქმებას ცდილობთ, კარგი ამბავი გვაქვს. ახლა სითხის გადასხმის შესახებ ამოცანის ამოსახსნელად რამდენიმე მარტივი ნაბიჯის დამახსოვრება საკმარისია. სანამ გიამბობთ, შეხედეთ, რა მოქმედებები შეგიძლიათ განახორციელოთ ორი ვედროთი. მათ გუნდები ვუწოდოთ და თითოეულს შემოკლებული მნიშვნელობა მივანიჭოთ.
- შდ – შეავსეთ წყლით დიდი ჭურჭელი
- შპ – შეავსეთ წყლით პატარა ჭურჭელი
- დდ – დაცალეთ დიდი ჭურჭელი
- დპ – დაცალეთ პატარა ჭურჭელი
- გდპ – გადაასხით წყალი დიდი ჭურჭლიდან პატარაში
- გპდ – გადაასხით წყალი პატარა ჭურჭლიდან დიდში
- დს? – შეამოწმეთ, სავსეა თუ არა დიდი ჭურჭელი
- პდ? –შეამოწმეთ, დაცლილია თუ არა პატარა ჭურჭელი
მოსახერხებელი რომ იყოს, კიდევ ერთი შემოკლება შემოვიღოთ. პირობითად ვედროში წყლის რაოდენობა ჩავწეროთ x:y, სადაც x ლიტრი წყალია პატარა ვედროში, ხოლო y – დიდში. ასე მაგალითად, ჩანაწერი 2:5 ნიშნავს, რომ პატარა ვედროში 2 ლიტრია, ხოლო დიდი – სავსეა.

ახლა ბლოკ–სქემა გამოვიყენოთ. თავიდან ორივე ვედრო ცარიელია, ანუ დავწეროთ 0:0. პატარა ვედრო ავავსოთ, მივიღებთ 3:0, პატარიდან დიდში გადავასხათ, გამოვა 0:3, შემდეგ სქემას მშვიდად მიყევით და არაფერზე ინერვიულოთ. მეთოდი მარტივი და საიმედოა, როგორც შვეიცარიული დანა. ყველა მოქმედების ჩანაწერი ქვემოთ მოცემულია:
0:0 — 3:0 — 0:3 — 3:3 — 1:5 — 1:0 — 0:1 — 3:1 — 0:4(!)
ერთადერთი მინუსი ისაა, რომ ამ სქემით ნაპოვნი გადაწყვეტილება ყოველთვის რაციონალური არ იქნება. მაგალითად, „კერკეტი კაკალის“ გმირს 2 ეტაპით ნაკლები დასჭირდა. როგორც უკვე გითხარით, დიდი ვედროთი დაიწყო და 6 გადასხმაში დაასრულა.
0:0 — 0:5 — 3:2 — 0:2 — 2:0 — 2:5 — 3:4(!)
მათემატიკური ბილიარდის მეთოდი
კითხვა, არის თუ არა ბილიარდი მათემატიკური თამაში, ღიად რჩება. ის, რომ თამაშის პრინციპი პუასონის ამოცანის ამოხსნის მეთოდზეა აწყობილი, ბევრს ამბობს. საბედნიეროდ, ჩვენ კიი არ დაგვჭირდება. ბურთებს ვირტუალურად გავაგორებთ. ამისთვის პარალელოგრამის ფორმის დახატულ ცხრილს გამოვიყენებთ.
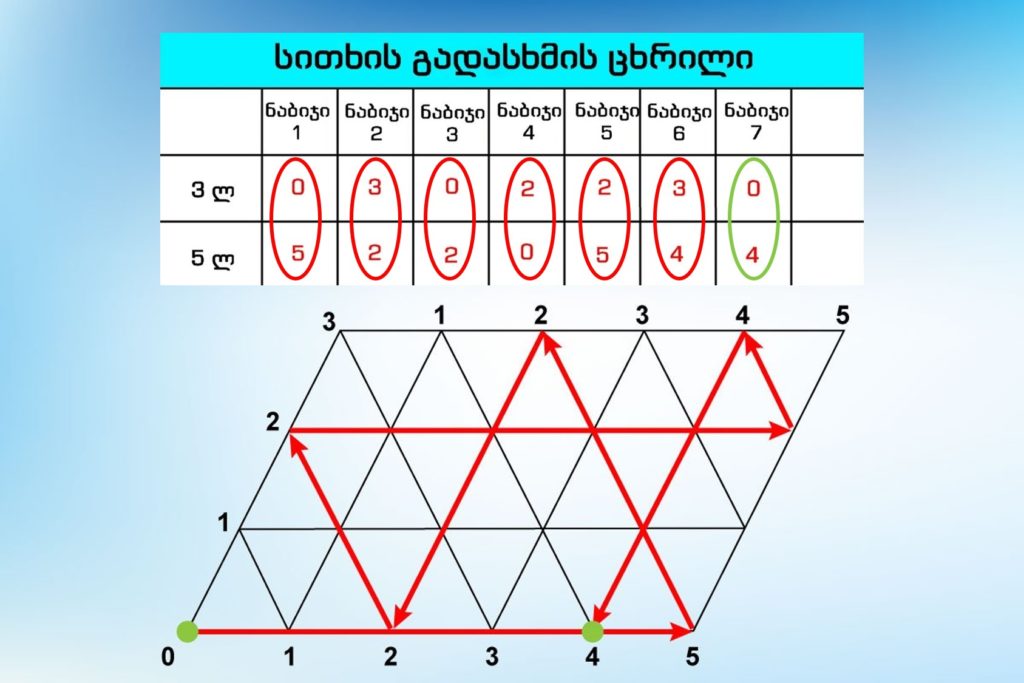
როგორც ხედავთ, მასზე დახაზული სწორი ხაზები ერთნაირ სამკუთხედების ბადეს ქმნის. ახლა მნიშვნელობის შესახებ. ადგილი, სადაც სამკუთხედის მწვერვალი ჩვენი „მაგიდის“ გვერდებს ეხება, ციფრებით აღნიშნულია. ამასთან, ჰორიზონტალურად გამოსახულია წყლის რაოდენობა ხუთლიტრიანებით, ხოლო ვერტიკალზე – სამლიტრიანი ჭურჭლით.

ბურთი გავუშვათ! თავიდან მარცხენა, ქვედა კუთხეში მდებარეობს და დარტყმის შემდეგ პარალელოგრამის ქვედა მხარის გასწვრივ „5“–ის წერტილამდე გადადის. გამოდის, რომ დიდ ვედროს ბოლომდე ვავსებთ. შემდეგ ბურთი ჰორიზონტალზე 2–ს და ვერტიკალზე 3–ს ეჯახება. გამოდის, რომ პატარა ვედრო სავსეა, დიდში 2 ლ წყალი დარჩა.
ბურთის შემდგომი გზის გაკვლევის და მისი მოძრაობის ყველა ეტაპის ჩაწერის შემდეგ მივიღებთ იგივე გამოსავალს, რაც მაკლენმა მოიფიქრა. თუ 0-დან ბურთი მოკლე მხარეს გადავიდა? თავად ნახეთ, რომ გამოსავალს იპოვით. უბრალოდ 2 ეტაპით მეტი დაგჭირდებათ, როგორც ჩვენი პირველი მცდელობის შემთხვევაში.
ამოცანა, რომელმაც პუასონი ცნობილი გახადა
დრო მოვიდა, ამოხსნათ ამოცანა, რომელმაც პუასონის ცხოვრება სამუდამოდ შეცვალა. შესაძლოა, თქვენც მათემატიკოსის ნიჭი აღმოაჩინოთ.

„ერთ ადამიანს ქილა 12 პინტა თაფლი აქვს და სურს, რომ ნახევარი თაფლი გააჩუქოს, მაგრამ 6 პინტიანი ქილა არ აქვს. აქვს 2 ცარიელი ჭურჭელი, ერთის მოცულობა 8 პინტა, მეორესი – 5. როგორ გადავასხათ მათი გამოყენებით ზუსტად 6 პინტა თაფლი?“
ზუსტად უცნობია, როგორ ამოხსნა ამოცანა პუასონმა. ჩვენი სტატიის წაკითხვის შემდეგ ცოდნით შეიარაღდით და იმედი გვაქვს, რომ ამოცანის ამოხსნა გაგიმარტივდებათ. ორიდან ერთი მეთოდი შეგიძლიათ აირჩიოთ. საქმეს შეუდექით!
პუასონის ამოცანის ამოხსნა
არ დაგავიწყდეთ, რომ ახლა პატარა ჭურჭელს 5 ლ მოცულობა აქვს, ხოლო დიდს – 8. ბლოკ–სქემა გამოვიყენე და 18 სვლის შემდეგ ამოვხსენი.
0:0 — 5:0 — 0:5 — 5:5 — 2:8 — 2:0 — 0:2 — 5:2 — 0:7 — 5:7 — 4:8 — 4:0 — 0:4 — 5:4 — 1:8 — 1:0 — 0:1 — 5:1 — 0:6(!)
ალბათ, ეს ყველაზე ოპტიმალური მოქმედების ეტაპები არაა. კარგად დაფიქრდით, რომ საუკეთესო სქემა გამოთვალოთ. სითხის გადასხმის შესახებ ამოცანები ლოგიკურ აზროვნებას, წარმოსახვას და შეუპოვრობას ავარჯიშებს. თავი პუასონის ადგილზე წარმოიდგინეთ და თქვენი აღმოჩენები გაგვიზიარეთ.









